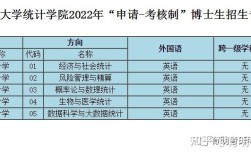
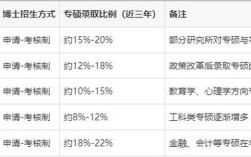
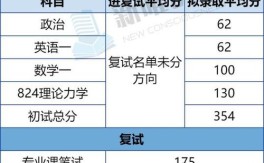
专业基础课和专业方向课,考试科目会根据你所报考的研究方向(导师)而有所不同。

考试科目概览
四川大学数学学院博士研究生入学考试的专业课,通常由以下科目组合而成:
-
专业基础课(必考):
- 数学分析
- 高等代数
这两门是数学学科的基础,几乎所有方向的考生都需要考。
-
专业方向课(二选一或多选一):
 (图片来源网络,侵删)
(图片来源网络,侵删)- 实变函数与泛函分析
- 常微分方程与偏微分方程
- 概率论与数理统计
- 计算数学
- 高等几何 / 复变函数 (根据具体方向要求)
具体考哪一门或哪几门,完全取决于你报考的导师及其研究方向。
考试科目详解及参考书目
以下是各个科目的详细说明和通常建议使用的参考书目。
专业基础课
① 数学分析
- :通常覆盖本科《数学分析》的核心内容,但深度和广度远超本科水平,重点包括:
- 极限、连续性、一致连续性
- 一致收敛性及其应用(函数项级数、含参积分)
- 多元微分学(隐函数定理、条件极值)
- 多元积分学(重积分、线面积分、场论初步)
- 含参变量积分(收敛性、可微性)
- Fourier级数与Fourier变换
- Lebesgue测度与积分(部分方向可能不要求,但了解有优势)
- 核心参考书目:
- 《数学分析》(上下册),陈纪修、於崇华、金路,高等教育出版社 (国内最主流、最经典的教材之一,内容详实,习题经典)
- 《数学分析》(上下册),华东师范大学数学系,高等教育出版社 (另一套经典教材,体系完整)
- 《数学分析新讲》(共三册),张筑生,北京大学出版社 (内容新颖,思想深刻,对提升思维能力非常有帮助)
- 《数学分析中的典型问题与方法》,裴礼文,高等教育出版社 (考研和考博的“神书”,包含大量难题和综合题,是强化训练的必备)
② 高等代数

- :同样要求对本科《高等代数》知识有极其深入的理解,重点包括:
- 多项式理论(整除、因式分解、根与系数关系)
- 行列式与线性方程组
- 矩阵理论(运算、秩、逆、相似、合同、Jordan标准形)
- 线性空间(基、维数、坐标、子空间、同构)
- 线性变换(核、像、特征值与特征向量、不变子空间)
- 双线性函数与欧几里得空间(内积、正交、正交变换、正交矩阵)
- 二次型(化标准形、正定性)
- 核心参考书目:
- 《高等代数》,北京大学数学系几何与代数教研室前代数小组,高等教育出版社 (俗称“北大蓝皮书”,国内最权威的高等代数教材)
- 《高等代数》,张禾瑞、郝鈵新,高等教育出版社 (另一套经典教材)
- 《高等代数解题方法》,钱吉林,湖北科学技术出版社 (与裴礼文的《数学分析》类似,是考研考博的习题集宝库)
- 《线性代数》,Gilbert Strang (Wellesley-Cambridge Press) (英文教材,视角独特,有助于加深对线性代数本质的理解)
专业方向课
① 实变函数与泛函分析
- 适用方向:泛函分析、调和分析、偏微分方程理论、应用数学理论等方向。
- :
- 实变函数:Lebesgue测度、可测函数、Lebesgue积分、收敛定理、Lp空间。
- 泛函分析:赋范线性空间、Banach空间、Hilbert空间、有界线性算子、共轭空间、谱理论初步。
- 核心参考书目:
- 《实变函数与泛函分析》(上下册),夏道行、严绍宗、吴卓人、舒五昌,高等教育出版社 (经典中的经典,内容全面,难度较高)
- 《实变函数论与泛函分析》(下册),程其襄、张奠宙、魏国强、胡善基、严绍宗,高等教育出版社 (内容精炼,条理清晰)
- 《Functional Analysis》, Peter D. Lax (Springer) (优秀的英文教材,思想深刻)
② 常微分方程与偏微分方程
- 适用方向:微分方程、动力系统、控制论等方向。
- :
- 常微分方程:基本理论(解的存在唯一性、延拓、稳定性)、定性理论(奇点、极限环)、边值问题。
- 偏微分方程:三类典型方程(波动、热传导、Laplace方程)的求解方法(分离变量法、积分变换法、基本解法)、特征线法、极值原理、能量方法、Sobolev空间初步。
- 核心参考书目:
- 《常微分方程》,王高雄、周之铭、朱思铭、王寿松,高等教育出版社 (国内最经典的常微分教材)
- 《常微分方程教程》,丁同仁、李承治,高等教育出版社 (内容更深入,适合备考)
- 《偏微分方程》,F. John (Springer) (经典的英文教材,侧重思想和理论)
- 《数学物理方程》,姜礼尚、陈亚浙、刘西垣、易法槐,高等教育出版社 (国内经典的数理方程教材)
③ 概率论与数理统计
- 适用方向:概率论、数理统计、随机过程、金融数学、生物统计等方向。
- :
- 概率论:概率空间、随机变量及其分布、数字特征、特征函数、极限定理(大数定律、中心极限定理)。
- 数理统计:参数估计(点估计、区间估计)、假设检验(Neyman-Pearson引理)、线性回归模型。
- 可能会涉及随机过程(如马尔可夫链、泊松过程)的基础知识。
- 核心参考书目:
- 《概率论与数理统计》,茆诗松、程依明、濮晓龙,高等教育出版社 (国内主流教材,内容全面)
- 《概率论基础》,李贤平,高等教育出版社 (侧重概率论的理论基础)
- 《概率论及其应用》,William Feller (Vol. 1 & 2) (概率论领域的“圣经”,内容博大精深)
- 《A Course in Probability Theory》, Kai Lai Chung (Academic Press) (非常经典的概率论研究生教材)
如何确定你的考试科目?
这是最关键的一步,直接决定了你的备考方向。
-
访问四川大学研究生院官网:
- 搜索“四川大学研究生院”,进入官网。
- 找到“招生工作”或“博士招生”栏目。
- 查找最新的《四川大学博士研究生招生专业目录》。
-
在专业目录中查找信息:
- 在目录中找到“数学学院”。
- 找到你感兴趣的专业代码(如070104 应用数学)和研究方向。
- 在该研究方向后面,会明确列出“考试科目”。
① 1001 英语② 2001 数学分析③ 2002 高等代数④ 2003 实变函数与泛函分析
- 这里的
2003就是你的专业方向课。
-
联系导师(非常重要):
- 在确定了大致方向后,最好能通过邮件等方式提前联系你心仪的导师。
- 在邮件中,可以礼貌地询问关于博士招生的具体事宜,包括考试科目的侧重点、参考书目的最新要求、对考生知识背景的期望等。
- 导师的回复往往是最权威、最直接的指导。
备考建议
- 基础为王:数学分析和高等代数是重中之重,必须花至少60%的时间来复习,做到概念清晰、定理证明熟练、基本运算准确无误。
- 精读教材,多做习题:不要只看不练,把推荐教材的课后习题至少做一遍,特别是裴礼文、钱吉林等辅导书上的难题,必须彻底搞懂。
- 重视证明题:博士考试非常看重逻辑推理和证明能力,对于每一个定理,不仅要会应用,更要理解其证明过程,并能独立复述。
- 关注前沿动态:在复习基础的同时,可以适当阅读一些你报考方向领域的综述性文章或经典论文,了解当前的研究热点,这对你复试和未来的研究都大有裨益。
- 信息渠道畅通:密切关注四川大学研究生院和数学学院的官网,及时获取招生简章、专业目录、考试大纲等官方信息。
- 提前准备英语:考博英语的难度不低,需要长期积累,尽早开始准备。
祝您备考顺利,成功上岸四川大学!