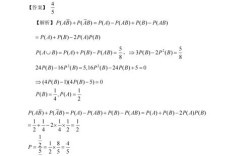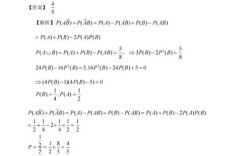2025年考研数学一真题作为当年研究生入学考试的重要参考,其命题特点、考查重点及难度分布对后续备考具有深远影响,该试卷高等数学占比56%,线性代数占比22%,概率论与数理统计占比22%,整体难度适中偏上,注重对基础知识综合运用能力及数学思维的考查,以下从试卷结构、典型题型分析及备考启示三个方面展开详细阐述。
试卷结构与考点分布
2025年数学一真题共23道题,包括8道选择题(每题4分,共32分)、6道填空题(每题4分,共24分)和9道解答题(共94分),各科目考点分布如下:
高等数学部分(约84分):
- 选择题:考查了极限计算(第1题)、导数定义(第2题)、二重积分(第3题)、微分方程(第4题)、级数收敛性(第5题)等,其中第1题涉及“1∞”型极限的求解,需结合等价无穷小与洛必达法则;第3题通过极坐标变换计算二重积分,凸显坐标系转换的重要性。
- 填空题:重点包括向量运算(第9题)、曲线积分(第10题)、幂级数收敛域(第11题)等,第10题对弧长的曲线积分需注意参数方程的选取,第11题需利用比值法确定收敛半径。
- 解答题:涵盖多元函数微分(第15题)、积分应用(第16题)、微分方程(第16题)、级数求和(第17题)等,其中第16题要求计算旋转体的体积与侧面积,综合考查定积分几何应用;第17题将幂级数与微分方程结合,需通过逐项求导建立方程并求解。
线性代数部分(约33分):
- 选择题:涉及矩阵秩(第5题)、特征值(第6题)、线性方程组解的结构(第7题),第6题需利用相似矩阵的性质判断特征值关系。
- 填空题:考查行列式计算(第13题),通过行列式性质展开简化运算。
- 解答题:重点为二次型标准化(第20题),需通过配方法或正交变换将二次型化为标准形,并判断二次型正定性,该题综合性较强,需综合运用特征值、特征向量等知识。
概率论与数理统计部分(约33分):
- 选择题:包括概率分布(第7题)、数字特征(第8题),第8题需利用协方差性质计算相关系数。
- 填空题:考查二维随机变量函数分布(第14题),需通过分布函数法求解。
- 解答题:涉及参数估计(第23题),要求验证估计量的无偏性并求最大似然估计,该题需掌握矩估计与最大似然估计的基本方法。
典型题型深度解析
极限与连续性(第1题)求极限 (\lim{x \to 0} \frac{\ln(\cos x)}{x^2})。 解析:该题为“0/0”型未定式,可采用洛必达法则或泰勒展开,使用洛必达法则时,分子导数为 (\frac{-\sin x}{\cos x} = -\tan x),分母导数为 (2x),再次应用洛必达法则得 (\lim{x \to 0} \frac{-\sec^2 x}{2} = -\frac{1}{2}),若用泰勒展开,(\ln(\cos x) = \ln(1 - \frac{x^2}{2} + o(x^2)) \approx -\frac{x^2}{2}),故极限为 (-\frac{1}{2}),本题考查极限计算的基本方法,需注意等价无穷小替换的条件。
多元函数微分学(第15题)设函数 (f(x,y)) 满足 (\frac{\partial f}{\partial x} = (2x + y^2)e^{x - y}),且 (f(0,y) = y + 1),求 (f(x,y))。 解析:由 (\frac{\partial f}{\partial x}) 积分得 (f(x,y) = \int (2x + y^2)e^{x - y} dx = e^{-y} \int (2x + y^2)e^{x} dx),利用分部积分,设 (u = 2x + y^2),(dv = e^{x} dx),则 (du = 2dx),(v = e^{x}),积分结果为 (e^{-y}[(2x + y^2 - 2)e^{x} + \phi(y)]),由初始条件 (f(0,y) = \phi(y) - 2e^{-y} + y + 1 = y + 1),得 (\phi(y) = 2e^{-y}),故 (f(x,y) = (2x + y^2 - 2 + 2e^{-y})e^{x - y}),本题综合考查偏积分与初始条件应用,需注意积分常数的处理。
线性代数二次型(第20题)设二次型 (f(x_1,x_2,x_3) = 2x_1^2 + x_2^2 - x_3^2 + 4x_1x_2 - 4x_1x_3),求正交变换将 (f) 化为标准形,并判断 (f) 是否正定。 解析:二次型矩阵为 (A = \begin{pmatrix} 2 & 2 & -2 \ 2 & 1 & 0 \ -2 & 0 & -1 \end{pmatrix}),特征方程 (|\lambda E - A| = 0) 解得特征值 (\lambda_1 = 1),(\lambda_2 = 3),(\lambda_3 = -2),对应特征向量经正交化单位化后得正交矩阵 (Q),标准形为 (f = y_1^2 + 3y_2^2 - 2y_3^2),因特征值有负,故 (f) 非正定,本题要求熟练掌握特征值、特征向量计算及正交变换方法。
备考启示与策略
- 夯实基础,注重概念:真题中约60%的题目直接考查基本概念和定理,如极限、导数、矩阵秩等,需吃透定义与性质,避免因概念模糊失分。
- 强化综合应用能力:如第17题级数与微分方程结合、第20题二次型与特征值综合,要求考生建立知识体系,跨章节灵活调用知识点。
- 重视计算训练:考研数学计算量较大,需通过大量练习提高运算速度与准确性,尤其注意积分、行列式等易错点。
- 研究真题规律:近五年真题中,高等数学占比稳定,极限、级数、微分方程为高频考点;线性代数侧重特征值与二次型;概率论重点在大数定律与参数估计。
相关问答FAQs
Q1:2025年数学一真题的难度如何?对不同层次考生有何影响?
A:2025年数学一整体难度适中,基础题约占50%,中档题30%,难题20%,对基础薄弱考生,重点抓好选择填空及解答题前几题,确保基本分;对中高水平考生,需攻克级数、微分方程等综合题,冲刺高分,试卷区分度较高,有利于高校选拔人才。
Q2:备考时如何高效利用2025年数学一真题?
A:建议分三阶段使用:第一轮按章节刷题,针对性训练考点(如用第1、11题练极限与级数);第二轮整套限时模拟,适应考试节奏;第三轮分析错题,总结命题陷阱(如第14题二维分布需注意积分区域划分),同时结合近年真题对比,把握趋势变化。