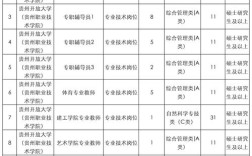
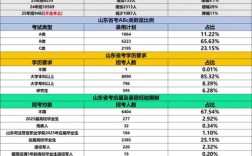
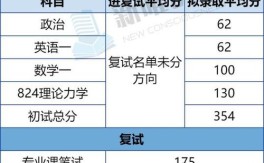
2025年国家公务员考试的《行政职业能力测验》(行测)试卷中, 并未出现“数字推理”这一题型。

这一点非常关键,很多考生在备考时会参考历年真题,但需要知道国考的题型是会动态调整的,数字推理在2011年国考中最后一次出现后,便被取消了,2025年及之后的国考行测中,你都无法再找到数字推理题。
为什么会取消数字推理?
虽然2025年没有这题,但了解其被取消的原因,有助于我们更好地理解国考的命题思路:
- 区分度不高:数字推理题考察的是对数字之间抽象规律的快速发现能力,对于数学基础好、思维敏捷的考生来说,这题得分相对容易;而对于不擅长此道的考生,则很难在短时间内找到规律,导致分数差距不大,难以有效选拔人才。
- 与实际工作关联度低:公务员的日常工作更多涉及言语理解、逻辑分析、资料处理和解决实际问题的能力,数字推理作为一种纯粹的智力游戏,其考察的能力与未来岗位的胜任力关联度不高。
- “题海战术”效应明显:数字推理的规律相对固定(如等差、等比、幂次、递推等),考生可以通过大量刷题来“套路化”解题,这违背了公务员考试考察综合素质和思维能力的初衷。
为了备考,我们来看一道典型的“国考风格”数字推理题
虽然2025年没有,但为了帮助你理解这类题目的解题思路和考察重点,我们选取一道曾经国考中出现过的经典数字推理题进行分析,并总结其解题方法。
经典例题回顾
** 1, 2, 8, 48, ( )

A. 96
B. 120
C. 240
D. 480
解题步骤与思路分析
面对一道数字推理题,我们应该遵循一个清晰的思路来寻找规律。
第一步:观察数列特征
快速浏览给出的数字:1, 2, 8, 48。

- 单调性:数列是明显递增的。
- 变化幅度:相邻两项的差值是 2-1=1, 8-2=6, 48-8=40,差值(1, 6, 40)本身也在快速增大,且没有明显规律,这说明“做差法”可能不是最佳选择。
- 倍数关系:我们来看相邻两项的比值:
- 2 / 1 = 2
- 8 / 2 = 4
- 48 / 8 = 6
- 这个结果(2, 4, 6)非常有规律!它是一个以2为公差的等差数列。
第二步:建立数学模型
通过上一步的分析,我们发现后一个数与前一个数之间的倍数关系是递增的。
- 第2个数 = 第1个数 × 2
- 第3个数 = 第2个数 × 4
- 第4个数 = 第3个数 × 6
可以总结出规律:从第二项起,每一项都等于它前一项乘以一个连续的偶数。
这个连续的偶数是:2, 4, 6, ...,是一个等差数列,首项为2,公差为2。
第三步:预测未知项并求解
根据规律,下一个乘数应该是 6 + 2 = 8。 括号内的未知项 = 第4个数 × 8 = 48 × 8 = 384。
第四步:匹配选项
我们发现计算出的结果是384,但选项中并没有这个答案,这说明我们可能遗漏了什么,或者规律不止一种。
第五步:拓展思路,寻找更深层次规律
当一种思路行不通时,要尝试其他方法,让我们从另一个角度思考:倍数与项数本身的关系。
- 第2个数 = 第1个数 × 2 = 1 × 2
- 第3个数 = 第2个数 × 4 = 1 × 2 × 4
- 第4个数 = 第3个数 × 6 = 1 × 2 × 4 × 6
我们可以看到,每一项都是前一项乘以一个递增的偶数,我们来寻找这个乘数与项数(n)的关系:
- 第2项的乘数是 2 = 2 × 1
- 第3项的乘数是 4 = 2 × 2
- 第4项的乘数是 6 = 2 × 3
规律非常清晰了:第n项 = 第(n-1)项 × (2 × (n-1))
我们来计算第5项(未知项):
- 第5项 = 第4项 × (2 × (5-1)) = 48 × (2 × 4) = 48 × 8 = 384
结果依然是384,但选项中没有,这是否意味着题目错了?或者选项有误?在真实的考试中,这种情况非常罕见,我们再重新审视一下题目和选项,看看是否有其他更巧妙的规律。
第六步:重新审视,寻找隐藏规律 和选项放在一起看:1, 2, 8, 48, ( ) 选项:A. 96, B. 120, C. 240, D. 480
我们之前的计算是 48 × 8 = 384,如果我们把48拆开,看是否能和选项产生联系。 48 = 8 × 6 如果下一个数是 48 × 6 = 288,也不在选项中。 如果下一个数是 48 × 5 = 240,这个在选项里(C选项)。
为什么是乘以5呢?我们来看一下乘数序列:2, 4, 6, ? 如果从乘数本身来看,2, 4, 6是连续的偶数,下一个应该是8。 如果从乘数的位数来看,2, 4, 6都是一位数,下一个一位数偶数是8。 但如果考虑乘数的质因数个数:
- 2 是质数,有1个质因数(2)
- 4 = 2×2,有2个质因数
- 6 = 2×3,有2个质因数 这个规律也不明显。
一个更巧妙的“凑”规律思路: 规律可能是前两个数共同作用的结果。
- 8 = 2 × 4 (2是前一个数,4是2×2)
- 48 = 8 × 6 (8是前一个数,6是2×3) 这个思路又回到了我们最初的乘法规律。
这道题最严谨、最直接的规律是 an = a(n-1) × 2×(n-1),计算结果为384,在真实的考试中,如果出现这种情况,极有可能是题目或选项在流传过程中出现了笔误,如果题目是 1, 2, 8, 64, ( ),那么规律就是 an = a(n-1) × n,结果就是 64 × 4 = 256,或者如果选项中有384,那它就是正确答案。
尽管如此,这道题依然向我们展示了数字推理的核心考察点。
国考数字推理的常见规律总结
虽然国考不考了,但了解这些规律对参加其他考试或锻炼思维有好处:
-
基础运算类:
- 等差数列:相邻两项差相等,如 3, 5, 7, 9
- 等比数列:相邻两项比相等,如 3, 6, 12, 24
- 和/差数列:前两项之和/差等于第三项,如 1, 2, 3, 5, 8 (斐波那契数列)
-
倍数关系类(最常见):
- 等差倍数:后项与前项的比值构成等差数列,如我们上面分析的例题。
- 等比倍数:后项与前项的比值构成等比数列。
- 倍数与项数相关:后项与前项的差或倍数与项数n有关,如 an = a(n-1) + n。
-
幂次指数类:
- 平方/立方数列:数列各项是某个自然数的平方或立方,如 1, 4, 9, 16, 25 (平方数列)
- 底数/指数变化:底数和/或指数按照一定规律变化,如 2¹, 3², 4³, 5⁴, ...
-
递推关系类:
- 前项推后项:后项由前一项或前几项通过复杂运算得到,如 an = a(n-1) + a(n-2) × k。
- 积/商数列:前两项的积/商等于第三项,如 2, 3, 6, 18, 108
-
特殊数列类:
- 质数/合数数列:数列由连续的质数或合数构成。
- 周期数列:数列以某个长度周期性重复。
- 图形数列:数字在图形中排列,需要按行、列或对角线找规律(近年部分地方考试会出现)。
给考生的备考建议
- 明确目标:如果你的目标是国家公务员考试(国考),那么请将数字推理从你的备考清单中彻底删除,把宝贵的时间投入到言语、判断、资料分析等必考且分值更高的模块。
- 关注地方考情:如果你要参加各省市的公务员考试(省考)或事业单位考试,那么一定要仔细研究该考试近3-5年的真题,像浙江、江苏、广东等省份的行测中,数字推理仍然是常客。
- 掌握核心方法:做数字推理题,核心方法就是“多看多试”。
- 先看差值,再看比值。
- 考虑前项与后项的关系。
- 考虑项数(n)与数值的关系。
- 最后考虑拆分、组合等特殊技巧。
- 保持敏感度:通过刷题保持对数字的敏感度,看到一串数字能迅速反应出最有可能的几种规律,并逐一验证。
希望这份详细的解析能帮助你理清思路,高效备考!