考研数学二是许多理工科和经管类考生必须面对的挑战,其考试范围和重点内容一直是备考者关注的焦点,在高等数学部分,二重积分作为多元函数积分学的重要组成部分,自然成为考生们关心的问题:考研数二是否考二重积分?答案是肯定的,二重积分不仅是考研数学二的考试内容,而且占据着不可忽视的地位,是每年命题的热点之一,下面将从考试大纲、考查形式、重点难点、备考策略等方面,对考研数二中的二重积分进行全面分析。
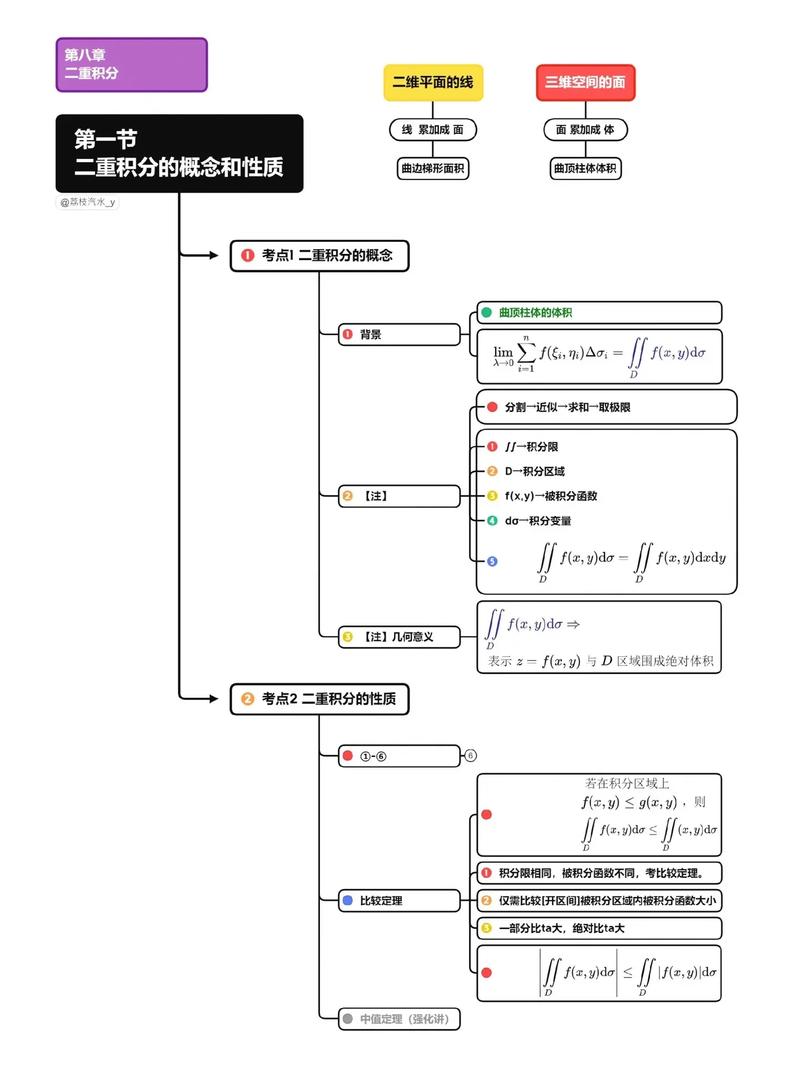
从考试大纲来看,考研数学二的考试内容明确包含多元函数微积分学,而二重积分正是该部分的核心知识点,根据教育部考试中心发布的《全国硕士研究生招生考试数学考试大纲》,数学二的高等数学部分要求考生掌握“二重积分的概念、基本性质和计算”,包括“利用直角坐标和极坐标计算二重积分”,以及“利用对称性简化二重积分计算”等内容,这一规定直接明确了二重积分在考研数二中的合法地位,意味着考生必须将其纳入复习范围,不可忽视,值得注意的是,数学二对多元函数积分学的要求相对数学一较低,不涉及三重积分、曲线积分和曲面积分等内容,这使得二重积分成为数学二多元函数积分学的唯一重点,其考查的深度和广度也因此更加集中。
从考查形式和分值占比来看,二重积分在考研数二中通常以客观题(选择题或填空题)和解答题的形式出现,在历年真题中,几乎每年都会有一道与二重积分相关的题目,分值约为10分左右,有时还会与其他知识点(如微分方程、级数等)结合,出现在综合性解答题中,题目可能要求考生通过计算二重积分来求某个平面图形的面积、某个立体的体积,或者求某个不均匀薄板的质量、质心等物理量,二重积分的计算还经常与极限、导数、积分等基础知识结合,形成对考生综合能力的考查,二重积分不仅是多元函数积分学的考点,更是连接基础知识与综合应用的桥梁,其重要性不言而喻。
二重积分的考查重点主要集中在以下几个方面:一是二重积分的概念和性质,包括积分的定义、线性性质、可加性、比较性质、估值性质和中值定理等,这些性质常常用于简化计算或判断积分的符号、范围;二是二重积分的计算方法,这是核心中的核心,包括直角坐标系下的计算(化为累次积分,确定积分限)和极坐标系下的计算(掌握极坐标与直角坐标的转换公式,以及极坐标下积分区域的表示和积分限的确定);三是利用对称性简化计算,这是二重积分计算的常用技巧,包括利用积分区域的对称性和被积函数的奇偶性,减少计算量,确定积分限是二重积分计算的难点和易错点,考生需要熟练掌握如何根据积分区域的边界曲线来确定累次积分的上限和下限,尤其是对于由多条曲线围成的复杂区域,更需要仔细分析。
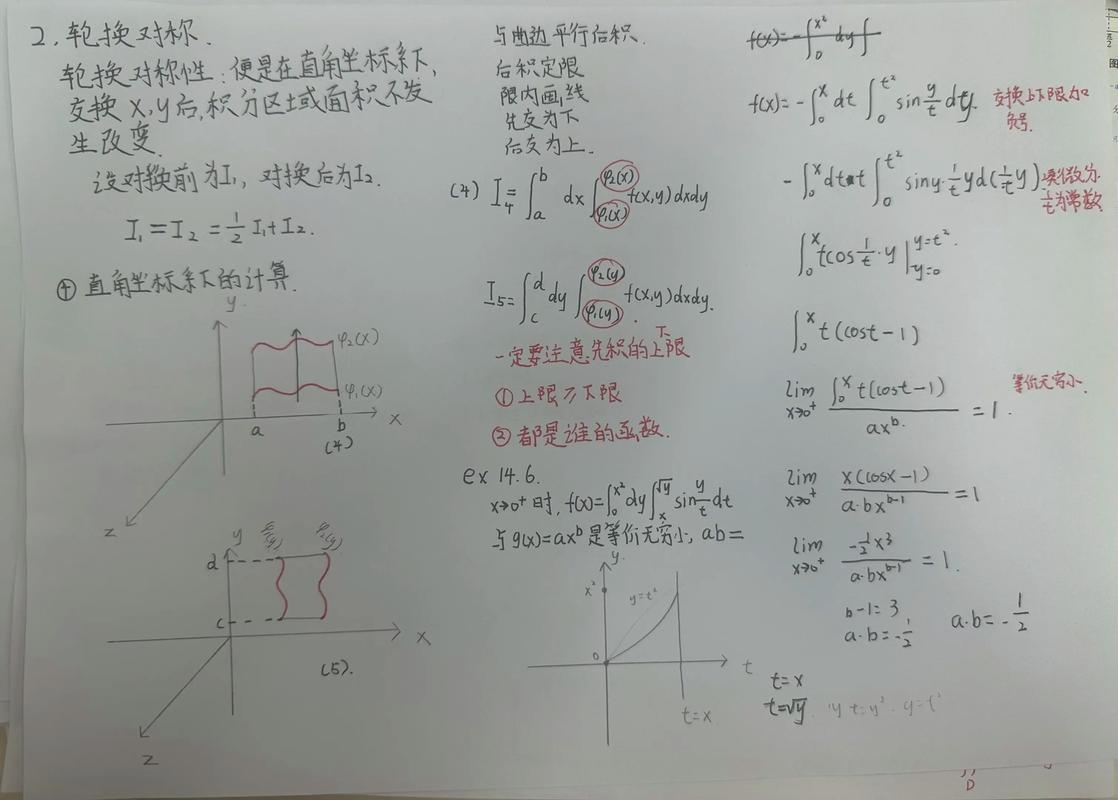
在备考过程中,针对二重积分这一知识点,考生应采取以下策略:第一,深刻理解概念,掌握性质,不仅要记住二重积分的定义和性质,更要理解其几何意义和物理意义,这样才能在遇到实际问题时灵活运用性质简化计算,第二,熟练掌握计算方法,尤其是直角坐标和极坐标下的计算技巧,对于直角坐标,要会根据积分区域的类型(X型区域或Y型区域)选择合适的积分次序;对于极坐标,要熟练掌握极坐标与直角坐标的转换公式(x=ρcosθ,y=ρsinθ,dxdy=ρdρdθ),并能准确将积分区域的边界方程转换为极坐标方程,第三,注重对称性的应用,对称性是简化二重积分计算的有效工具,考生需要总结归纳常见的对称情形,例如积分区域关于x轴对称、关于y轴对称、关于原点对称等,以及被积函数相应具有奇偶性时的简化结果,第四,加强习题训练,提高计算能力,二重积分的计算往往涉及大量的积分运算,考生需要通过做一定数量的习题,熟练掌握各种积分技巧,提高计算的准确性和速度,建议考生从基础题入手,逐步过渡到综合题和难题,重点关注历年真题中的二重积分题目,分析其命题规律和解题思路。
为了更直观地展示二重积分在考研数二中的考查重点,以下表格总结了核心知识点及常见考查形式:
| 核心知识点 | 常见考查形式 | |
|---|---|---|
| 二重积分的概念与性质 | 定义、几何意义、物理意义、线性性质、可加性、比较性质、估值性质、中值定理 | 利用性质判断积分大小、确定积分符号、估计积分值 |
| 直角坐标系下的计算 | X型区域、Y型区域的划分,累次积分的设置,积分限的确定 | 计算给定直角坐标区域上的二重积分,交换积分次序 |
| 极坐标系下的计算 | 极坐标与直角坐标的转换,极坐标下积分区域的表示(如圆、圆环、扇形等) | 计算给定极坐标区域(或适合用极坐标计算)上的二重积分 |
| 对称性的应用 | 积分区域关于x轴、y轴、原点对称,被积函数的奇偶性 | 利用对称性简化积分计算,减少计算量 |
| 综合应用 | 二重积分与几何(面积、体积)、物理(质量、质心、转动惯量)的结合 | 结合实际问题或与其他知识点(如微分方程)结合,出现在综合性解答题中 |
二重积分是考研数学二中的必考内容,其重要性和考查特点决定了考生必须给予足够的重视,在复习时,考生应紧扣考试大纲,深入理解概念,熟练掌握计算方法,尤其是直角坐标和极坐标下的计算技巧,以及对称性的应用,并通过大量习题训练提高综合运用能力,才能在考试中从容应对二重积分相关的题目,为取得优异成绩奠定基础。
相关问答FAQs:
问题1:考研数二二重积分的计算中,如何选择直角坐标还是极坐标?
解答:选择坐标系主要根据积分区域的边界曲线和被积函数的形式,如果积分区域的边界曲线由圆、圆弧、直线或射线组成,且被积函数中含有x²+y²的形式,优先考虑极坐标,因为极坐标下可以简化积分区域和被积函数的表达式,使计算更简便,计算由x²+y²=1所围成的区域上的二重积分时,极坐标下的积分区域表示为ρ∈[0,1],θ∈[0,2π],远比直角坐标下的X型或Y型区域划分简单,反之,如果积分区域的边界曲线主要由直线、抛物线、双曲线等非圆弧曲线组成,且被积函数不含x²+y²项,通常采用直角坐标计算,有时需要根据被积函数的形式灵活选择,例如被积函数为f(x²+y²)时,极坐标下的被积函数变为f(ρ²),积分过程可能更简单。

问题2:在确定二重积分的积分限时,容易出现哪些错误?如何避免?
解答:确定积分限时常见的错误包括:一是积分次序选择不当,导致积分限表达复杂或无法计算,对于既不是X型也不是Y型的区域,需要将其分割成若干个子区域,分别确定积分限,若强行选择一种积分次序,可能会导致计算困难或错误,二是积分限的上下限颠倒,尤其是在极坐标下,容易忽略ρ的下限是否为0,或θ的范围是否正确(如θ的起始角度和终止角度),三是对于由参数方程或隐式方程表示的边界曲线,未能正确将其转化为积分限的表达式,为了避免这些错误,考生应首先画出积分区域的草图,直观地判断区域的类型;根据区域的边界曲线选择合适的积分次序,必要时进行分割;严格按照定义确定积分限,例如在直角坐标下,X型区域的y积分下限是下边界曲线,上限是上边界曲线,x积分限是区域的最左和最右端点;在极坐标下,ρ的积分限通常是从极点出发的射线与边界曲线的交点,θ的积分限是射线扫过区域的角度范围,通过交换积分次序或验证特殊点的方法检查积分限的正确性。