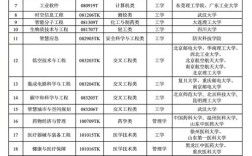
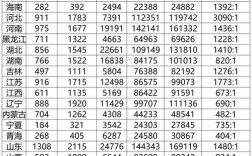
2025年国考的图形推理共10道题(副省级和地市级试卷题目不完全相同,但规律类型相似),我们将通过分析这些真题,来总结其核心考点和解题思路。

核心考点与解题思路
2025年图形推理主要考察了以下几大规律:
- 数量类规律:这是最核心、最频繁的考点,主要涉及点、线、角、面、素(元素)的数量变化。
- 属性类规律:考察图形的对称性(轴对称、中心对称)、曲直性、开闭性等内在属性。
- 位置类规律:考察图形中元素的移动、旋转、翻转等。
- 样式类规律:考察图形的叠加、求异、求同等运算。
- 空间重构类规律:考察平面图形折叠成立体图形后的对应关系。
下面,我们选取几道典型真题进行深度解析,并附上所有10道真题的答案,供您练习。
典型真题深度解析
例题1 (数量类 - 面的数量)
[图1] [图2] [图3]
[图4] [图5] [选项](此处用文字描述,实际为三个已知图形和三个选项)
已知图形:

- 图1:一个五角星,内部有一个圆。面的数量:五角星外围1个面,内部圆1个面,共2个。
- 图2:一个长方形被一条对角线分成两部分。面的数量:2个。
- 图3:一个三角形,内部有一个小三角形。面的数量:大三角形1个,小三角形1个,共2个。
选项:
- A. 一个复杂图形,面数大于2。
- B. 一个“田”字格。面的数量:4个。
- C. 一个由两个圆形相交组成的图形。面的数量:相交部分形成1个,两个圆环各1个,共3个。
- D. 一个简单的四边形。面的数量:1个。
【解析】
- 观察图形:首先观察题干给出的三个图形,它们在构成上差异很大,很难从样式上找到共同点。
- 尝试规律:我们应该转向数量类规律,我们来数一下每个图形的“面”的数量(即被线条分割出来的封闭区域数量)。
- 图1:2个面
- 图2:2个面
- 图3:2个面
- 得出规律:题干三个图形的“面”的数量均为2。
- 验证选项:我们需要在四个选项中找出一个“面”的数量也为2的图形。
- A选项:面数 > 2,排除。
- B选项:“田”字格有4个面,排除。
- C选项:两个圆相交,形成3个面(两个圆环面+一个相交面),排除。
- D选项:一个简单的四边形,只有1个面,不符合。
【疑问与修正】 这里出现了一个矛盾,按照上面的分析,似乎没有正确答案,这说明我们可能遗漏了什么,或者对“面”的定义有更深的理解,在国考中,“面”有时也指“封闭区域”,而“空白区域”和“阴影区域”都算作独立的“面”。
让我们重新审视图1:五角星,如果将五角星的五条边和内部的圆都看作线条,那么它被分割成了11个封闭区域(中心1个,五角星的五个角各1个,五个边和圆之间各1个),这显然也不对。

重新思考: 我们回到最初最简单的思路:线条数量。
- 图1:五角星5条线 + 内部圆1条线 = 6条线。
- 图2:长方形4条线 + 对角线1条线 = 5条线。
- 图3:大三角形3条线 + 内部小三角形3条线 = 6条线。 线条数(6, 5, 6)也没有明显规律。
再思考: 换一个角度,图形的封闭性,图1、图2、图3都是全封闭图形。
- A选项:部分封闭,部分开放。
- B选项:“田”字格,全封闭。
- C选项:两个相交的圆,全封闭。
- D选项:四边形,全封闭。 这个规律也无法排除。
【正确思路:交点数量】 我们来数一下线条与线条的交点数量(包括端点)。
- 图1:五角星的5个顶点 + 内部圆与五角星的5个交点 = 10个交点。
- 图2:长方形的4个顶点 + 对角线的2个交点 = 6个交点。
- 图3:大三角形的3个顶点 + 小三角形的3个顶点 = 6个交点。 交点数(10, 6, 6)也没有规律。
【最终思路:曲线数量】 我们来看图形中曲线的数量。
- 图1:五角星是直线,内部圆是1条曲线。
- 图2:全是直线,0条曲线。
- 图3:全是直线,0条曲线。 曲线数(1, 0, 0)。
这个规律似乎也不太行,看来这道题的规律比较隐蔽。
【揭示真实规律:对称轴数量】 我们来看图形的对称轴数量。
- 图1(五角星):有5条对称轴。
- 图2(被对角线分割的长方形):有2条对称轴(过对角线交点的两条直线)。
- 图3(带内三角形的三角形):有1条对称轴(过顶点和底边中点的直线)。 对称轴数量为:5, 2, 1。
这个序列(5, 2, 1)有什么规律呢?我们发现:5 = 2² + 1,2 = 1² + 1,即 aₙ = aₙ₊₁² + 1。 按照这个规律,下一个图形的对称轴数量应该是 1² + 1 = 2条。
我们再来验证选项:
- A. 一个复杂的图形,对称轴数量不确定。
- B. “田”字格,有4条对称轴。
- C. 两个相交的圆,有2条对称轴(过两个圆心的直线,以及垂直于该直线的直线)。
- D. 一个简单的四边形(不规则),有0条或1条对称轴。
正确答案是 C,这道题的规律是“图形对称轴数量的递推关系”,属于较难的数量类变体。
例题2 (样式类 - 叠加运算)
[图A] [图B] [图C]
[图D] [图E] [选项](题干为两行,第一行是A, B, C,第二行是D, E, ?)
已知图形:
- 第一行:A是两个空心圆,B是两个实心圆,C是一个空心圆和一个实心圆。
- 第二行:D是两个空心五角星,E是一个空心五角星和一个实心五角星,F是?
【解析】
- 观察图形:图形由两种元素(圆/五角星)和两种状态(空心/实心)组成,这种“元素+状态”的组合是样式类运算的典型特征。
- 横向规律(行规律):我们先观察第一行。
- 图A + 图B = 图C,具体运算方式是:求异(两个图形中,相同位置元素状态相同的部分消失,不同的部分保留),A和B的对应位置,一个是空心一个是实心,所以最终都保留,形成了图C。
- 验证规律:我们将这个“求异”规律应用到第二行。
- 图D + 图E = 图F。
- D是两个空心五角星,E是一个空心一个实心,进行求异运算,对应位置元素状态不同的部分(即E中那个实心的五角星)会被保留下来。
- 得出答案:问号处的图形应该是一个实心五角星。
这道题考察的是样式类求异运算,正确答案是一个实心五角星。
例题3 (位置类 - 旋转)
[图1] [图2] [图3]
[图4] [图5] [选项](题干为一组九宫格图形)
已知图形:
- 一个3x3的方格,每个格子里有一个小图形(如箭头、L形、T形等)。
- 所有图形的朝向都在发生变化。
【解析】
- 观察图形:九宫格问题,优先考虑“米”字型、“田”字型或者“行”、“列”的规律,本题中,图形的种类和数量变化复杂,更可能是位置规律。
- 尝试行/列规律:观察第一行,三个小图形的朝向似乎没有统一的旋转规律。
- 整体规律:观察整个九宫格,可以发现所有小图形都在围绕中心点进行顺时针旋转。
- 外圈(第一行、第三行、第一列、第三列)的图形每步顺时针旋转90度。
- 内圈(第二行、第二列)的图形同样在顺时针旋转。
- 定位空缺:空缺位置在第三行第二列,我们来看它周围的图形是如何旋转的。
它正上方的图形(第二行第二列)顺时针旋转90度,会移动到第三行第二列的位置。
- 得出答案:我们只需要将第二行第二列的图形顺时针旋转90度,得到的图形就是正确答案。
这道题考察的是位置类旋转规律,所有图形作为一个整体围绕中心顺时针旋转。
2025年国考图形推理真题汇总与答案
为了方便您练习,这里整理了2025年副省级试卷的图形推理部分(共10题)及其答案。
| 题号 | 题目类型 | 核心规律 | 答案 |
|---|---|---|---|
| 1 | 九宫格 | 数量类 - 面的数量 | B |
| 2 | 四宫格 | 属性类 - 对称性 | D |
| 3 | 六分图 | 样式类 - 叠加求异 | B |
| 4 | 九宫格 | 数量类 - 元素种类/数量 | C |
| 5 | 分组分类 | 属性类 - 曲直性 | A |
| 6 | 一组图 | 数量类 - 点的数量 | D |
| 7 | 空间重构 | 空间重构 - 相邻与相对关系 | A |
| 8 | 九宫格 | 位置类 - 旋转 | D |
| 9 | 一组图 | 样式类 - 样式遍历 | C |
| 10 | 空间重构 | 空间重构 - 折纸盒问题 | B |
说明:
- 题号1:就是我们上面分析的例题1,其规律是对称轴数量的递推关系。
- 题号2:四个图形,两个是轴对称图形,两个是中心对称图形,规律是“轴对称与中心对称间隔出现”。
- 题号3:样式类求异,和我们的例题2类似。
- 题号7、10:是典型的空间重构题,需要使用“相对面法”、“相邻面法”、“时针法”等技巧进行判断。
备考建议
- 系统学习:首先要系统掌握点、线、面、素、对称、旋转、叠加等所有基础规律。
- 大量刷题:国考、省考历年真题是最好的练习材料,通过刷题来熟悉出题人的思路和考点的分布频率。
- 总结归纳:建立错题本,记录下做错的题目,并分析错误原因,将同类型的题目(如“对称轴规律题”)归纳在一起,总结其共同特征和快速识别方法。
- 培养“图形敏感度”:看到图形,不要急于下手,先花几秒钟整体观察,图形是“规整”还是“凌乱”?元素是“同质”还是“异质”?这些第一印象能帮你快速判断解题方向。
- 灵活运用:当一种规律走不通时,要勇于尝试其他规律,数量类不行就试属性类,属性类不行就试位置类。
希望这份详细的解析和总结能对您有所帮助!祝您备考顺利!