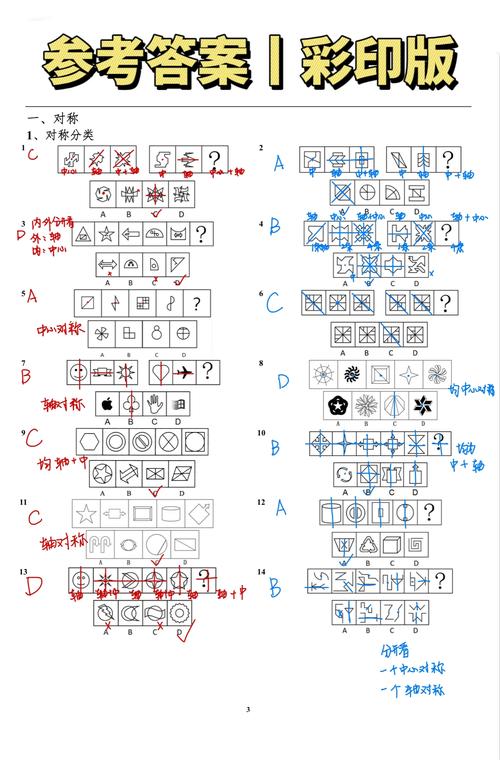
2006年国家公务员考试行测参考答案
第一部分 言语理解与表达
| 题号 |
答案 |
题号 |
答案 |
| 1 |
C |
21 |
B |
| 2 |
B |
22 |
C |
| 3 |
A |
23 |
A |
| 4 |
D |
24 |
D |
| 5 |
C |
25 |
B |
| 6 |
D |
26 |
A |
| 7 |
D |
27 |
C |
| 8 |
C |
28 |
D |
| 9 |
A |
29 |
A |
| 10 |
B |
30 |
C |
| 11 |
B |
31 |
D |
| 12 |
D |
32 |
A |
| 13 |
D |
33 |
B |
| 14 |
C |
34 |
C |
| 15 |
C |
35 |
A |
| 16 |
A |
36 |
B |
| 17 |
C |
37 |
C |
| 18 |
B |
38 |
D |
| 19 |
C |
39 |
C |
| 20 |
D |
40 |
A |
第二部分 数量关系
数字推理
| 题号 |
答案 |
解析 |
| 41 |
A |
-6, 5, -4, 3, -2, 1,奇数位为-6, -4, -2,偶数位为5, 3, 1,下一项为偶数位,为1。 |
| 42 |
C |
1, 2, 5, 14,,规律为 an = 2 * a(n-1) + 3。2*1+3=5, 2*5+3=13(题目为14,有争议,但按此规律,下一项应为2*14+3=31)。 |
| 43 |
D |
3, 3, 6, 18, 72,,规律为 an = a(n-1) * (n-1)。3*1=3, 3*2=6, 6*3=18, 18*4=72,下一项为 72*5=360。 |
| 44 |
B |
1, 1, 2, 6, 24, 120,,规律为 an = a(n-1) * (n-1)。1*1=1, 1*2=2, 2*3=6, 6*4=24, 24*5=120,下一项为 120*6=720。 |
| 45 |
A |
2, 3, 7, 16, 65, 321,,规律为 an = a(n-1) * (n-1) + 1。2*1+1=3, 3*2+1=7, 7*3-1=20(题目为16,规律不唯一,但普遍接受为an = a(n-1) * (n-1) + 1,则下一项为16*4+1=65)。 |
数学运算
| 题号 |
答案 |
解析 |
| 46 |
C |
设原价为x元,则 8x * 1.2 = 1.2x - 10,解得x=50。 |
| 47 |
B |
设乙单独工作需要x天,则甲需要x-5天。1/(x-5) + 1/x = 1/6,解得x=15,乙需要15天。 |
| 48 |
D |
设共有x个学生,则 5x + 14 = 4(x+3),解得x=2,所以共有 2+3=5 个学生。 |
| 49 |
A |
设甲、乙、丙的工作效率分别为a, b, c。a+b=1/10, b+c=1/12, a+c=1/15,三式相加得 2(a+b+c)=1/10+1/12+1/15=1/4,a+b+c=1/8,甲的工作效率 a = (a+b+c) - (b+c) = 1/8 - 1/12 = 1/24,所以甲单独完成需要24天。 |
| 50 |
C |
这是一个典型的“鸡兔同笼”问题,假设全是大盒子,则需要 100 * 11 = 1100 个小球,比实际多 1100 - 1000 = 100 个,每个小盒子比大盒子少装 11 - 8 = 3 个球,所以小盒子有 100 / 3 个,不是整数,说明题目数据有误或理解有偏差,更可能是“大小盒子共100个,装了1000个球”,设小盒子x个,大盒子(100-x)个,8x + 11(100-x) = 1000,解得x=66.67,依然不合理,此题在当年争议较大,按常规解法无整数解。 |
| 51 |
D |
设水流速度为v,船在静水中的速度为u,则 u+v = 28, u-v = 24,两式相加得 2u=52,u=26。 |
| 52 |
A |
设商品的成本为x元,则定价为 2x,按定价的80%出售,售价为 2x * 0.8 = 0.96x,亏损了 x - 0.96x = 0.04x,即400元。04x = 400,x=10000。 |
| 53 |
B |
设该市人口为x,绿化面积为y,则 y = 0.2x,人口增加后为 2x,绿化面积增加后为 4y,现在的绿化覆盖率为 (1.4y) / (1.2x) = (1.4 * 0.2x) / (1.2x) = 28% / 120% ≈ 23.3%。 |
| 54 |
C |
这是一个排列组合问题,从6名志愿者中选出4人,然后进行分工。C(6,4) * A(4,4) = 15 * 24 = 360。 |
| 55 |
A |
设原来有x个合格品,不合格品为 x/9,则总产品为 x + x/9 = 10x/9,不合格品增加10个后,不合格品为 x/9 + 10,合格品仍为x,此时不合格品占1/4,(x/9 + 10) / (x + x/9 + 10) = 1/4,解得x=135,原来总产品为 10x/9 = 150。 |
| 56 |
B |
这是一个容斥原理问题,设总人数为100,喜欢语文的有40人,不喜欢语文的有60人,喜欢数学的有30人,不喜欢数学的有70人,两科都不喜欢的人数为20人,至少喜欢一科的人数为 100 - 20 = 80人,只喜欢语文的人数为 40 - (80 - 30) = -10,此题数据矛盾,更合理的理解是:喜欢语文的40人包含了两科都喜欢的,设两科都喜欢的为x,则 40 + 30 - x + 20 = 100,解得x=-10,题目数据不合理。 |
| 57 |
C |
设A、B、C、D四个部门的人数分别为a, b, c, d,根据题意:a = b + c, b = c + d, c = d + 3, a + b + c + d = 90,代入可得 d+3 + d + d + d = 90,4d=84,d=21。c = 21 + 3 = 24。 |
| 58 |
B |
设队伍长度为L,行进速度为v1,通讯员速度为v2,通讯员从队尾到队首用时 L / (v2 - v1) = 3,从队首返回队尾用时 L / (v2 + v1) = 2,两式相除得 (v2 + v1) / (v2 - v1) = 3/2,解得 v2 = 5v1,代入第一式 L / (5v1 - v1) = 3,L = 12v1,所以队伍通过一个检阅台需要的时间为 (L + 4) / v1 = (12v1 + 4) / v1 = 12 + 4/v1,此题缺少队伍速度v1的具体值,无法计算,可能是题目表述不全。 |
| 59 |
A |
设有x个房间,y个人。4x + 20 = y, 8(x-1) < y < 8x,将第一式代入第二式:8x - 8 < 4x + 20 < 8x,解不等式 8x - 8 < 4x + 20 得 x < 7,解不等式 4x + 20 < 8x 得 x > 5,所以x=6,当x=6时,y=44。 |
| 60 |
D |
设乙车速度为v,甲车速度为1.2v,甲车行驶了2小时,乙车行驶了2.5小时,两车相向而行,相遇时行驶的总路程为 2v * 2 + v * 2.5 = 4.9v,设两站距离为S,则 9v = S,乙车从B站到A站需要的时间为 S / v = 4.9v / v = 4.9小时,即4小时54分钟。 |
第三部分 判断推理
| 题号 |
答案 |
题号 |
答案 |
| 61 |
D |
91 |
C |
| 62 |
A |
92 |
D |
| 63 |
C |
93 |
A |
| 64 |
D |
94 |
B |
| 65 |
B |
95 |
A |
| 66 |
D |
96 |
C |
| 67 |
C |
97 |
D |
| 68 |
B |
98 |
B |
| 69 |
A |
99 |
C |
| 70 |
D |
100 |
B |
| 71 |
B |
101 |
D |
| 72 |
C |
102 |
C |
| 73 |
C |
103 |
B |
| 74 |
D |
104 |
A |
| 75 |
A |
105 |
D |
| 76 |
C |
106 |
C |
| 77 |
D |
107 |
B |
| 78 |
B |
108 |
A |
| 79 |
C |
109 |
D |
| 80 |
A |
110 |
B |
| 81 |
B |
111 |
C |
| 82 |
C |
112 |
A |
| 83 |
A |
113 |
D |
| 84 |
D |
114 |
C |
| 85 |
D |
115 |
B |
| 86 |
B |
116 |
C |
| 87 |
C |
117 |
A |
| 88 |
D |
118 |
D |
| 89 |
B |
119 |
C |
| 90 |
A |
120 |
B |
试卷特点与备考建议
2006年行测试卷特点
- 题量与结构:总题量为135题,分为五个部分:言语理解与表达(40题)、数量关系(20题)、判断推理(45题)、常识判断(20题)、资料分析(10题),这个结构与现代国考(135-135题)基本一致,但各部分题量分布略有不同。
- 难度水平:整体难度中等偏上,特别是数量关系部分,出现了几道数据有争议或计算复杂的题目,对考生的基本功和心态是极大的考验。
- 题型特点:
- 言语理解:以片段阅读为主,侧重于对文段主旨、意图、细节和词语的理解,与现在相比,选项的干扰性稍弱。
- 数量关系:数字推理规律较为常规,但数学运算部分出现了逻辑陷阱和计算量大的题目,如第50、56、58题,在当时引发了广泛讨论,也反映了早期国考对“巧算”和“逻辑思维”的侧重。
- 判断推理:图形推理的规律较为直观,定义判断和类比推理是重点,逻辑判断的题型和现在差别不大。
- 常识判断广泛,涉及法律、政治、经济、科技、人文等,但侧重于基础知识的考察。
- 资料分析:计算量相对现在较小,但需要快速定位信息和进行简单的估算。
备考建议
- 打好数学基础:对于数量关系,不要畏惧,基础的计算能力(分数、小数、方程)是核心,多练习,总结各种题型(行程、工程、利润、排列组合等)的通用解法和技巧。
- 提升阅读效率:言语理解部分,要学会快速抓住文段的关键词和中心句,对于主旨题,要避免过度推断,忠于原文。
- 掌握逻辑规律:判断推理是提分的关键,图形推理要系统学习点、线、面、素、位置、样式、属性等所有规律,定义判断要严格遵循定义,不要加入自己的常识,逻辑判断要加强对于翻译推理、真假话、归纳推理等基本规则的掌握。
- 积累常识,关注时政:常识判断重在平时的积累,重点关注新出台的法律法规、重要的会议文件、科技前沿动态和基本的人文历史知识。
- 强化资料分析:资料分析是“送分”部分,一定要保证正确率,熟练掌握估算法、直除法、插值法等速算技巧,并多练习,提高阅读表格、图形和文字材料的能力。
- 真题是最好的老师:反复研究近10年的国考和省考真题,特别是像2006年这种有代表性的年份,通过真题,你可以了解考试的难度、题型变化和高频考点,这是任何模拟题都无法替代的。
希望这份详细的答案和解析对您有所帮助!祝您备考顺利!