考研数学分为数学一、数学二和数学三,三者适用专业、考试范围、难度要求及侧重点均存在显著差异,考生需根据自身报考专业选择对应的考试类型,针对性备考,以下从适用专业、考试内容、难度差异及备考建议四个维度展开详细分析。
适用专业不同:专业特性决定考试类型
考研数学的分类核心依据是报考专业的学科特点及对数学能力的要求,三者覆盖了从理工到经管再到部分交叉学科的不同需求。
数学一主要面向对数学要求较高的理工类专业,通常包括:
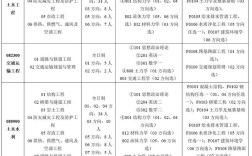
- 学科门类为“工学”的一级学科,如力学、机械工程、光学工程、仪器科学与技术、冶金工程、动力工程及工程热物理、电气工程、电子科学与技术、信息与通信工程、控制科学与工程、计算机科学与技术、土木工程、水利工程、测绘科学与技术、交通运输工程、船舶与海洋工程、航空宇航科学与技术、兵器科学与技术、核科学与技术、生物医学工程等;
- 部分理学专业,如数学、物理学、化学(部分方向)、地质学、地理学、地球物理学、生物学(部分方向)等;
- 管理学中的“管理科学与工程”(一级学科,可授管理学、工学学位)。
这类专业往往涉及复杂的工程问题、理论推导或大规模计算,需要考生具备扎实的数学理论基础和综合应用能力。
数学二适用范围相对聚焦,主要面向对数学要求较低的部分理工类专业,包括:

- 工学门类中的纺织科学与工程、轻工技术与工程、农业工程、林业工程、食品科学与工程等一级学科;
- 部分理工科院校的特色专业,如材料科学与工程、环境科学与工程(部分方向)、生物工程等。
数学二不考察概率论与数理统计,且高等数学的考试范围较数学一大幅缩减,更侧重基础计算和应用能力。
数学三则专为经管类专业设计,适用学科包括:
- 经济学门类中的理论经济学、应用经济学(一级学科);
- 管理学门类中的工商管理、农林经济管理(一级学科);
- 部分专业硕士,如金融、应用统计、税务、国际商务、保险、资产评估等。
经管类专业的研究常涉及数据分析、模型构建,数学三侧重微积分、线性代数与概率论在经济问题中的应用,难度低于数学一,但更注重实际问题的数学建模能力。
与范围差异:知识模块与侧重点不同
数学二、数学三在考试内容上均包含高等数学(微积分)、线性代数,但数学三增加概率论与数理统计,且高等数学、线性代数的具体考点范围存在差异,以下通过表格对比三者的内容分布:
| 科目模块 | 数学一 | 数学二 | 数学三 |
|---|---|---|---|
| 高等数学 | 内容最全,包括函数、极限、连续、一元函数微积分、多元函数微积分、无穷级数、常微分方程等,多元函数微积分含三重积分、曲线曲面积分;无穷级数含傅里叶级数;常微分方程含可降阶方程、线性微分方程等。 | 范围最小,不考察三重积分、曲线曲面积分、无穷级数(仅要求常数项级数的审敛性)、傅里叶级数;常微分方程仅要求一阶、二阶(可降阶除外)。 | 与数学一的高等数学部分内容基本一致,但侧重点不同:如多元函数微积分不要求三重积分的应用(仅计算),无穷级数不要求傅里叶级数,常微分方程要求与经济模型相关的简单应用。 |
| 线性代数 | 内容全面,包括行列式、矩阵、向量、线性方程组、特征值与特征向量、二次型等,注重理论推导和综合应用(如向量组的线性相关性、矩阵的相似对角化等)。 | 与数学一基本一致,但部分考点要求降低:如二次型仅要求标准形、规范形,不要求合同变换;特征值与特征向量不要求实对称矩阵的性质。 | 内容与数学一基本重合,但更侧重矩阵运算、线性方程组求解及经济模型中的应用(如投入产出模型),对理论深度要求略低于数学一。 |
| 概率论与数理统计 | 包括随机事件与概率、随机变量及其分布、多维随机变量及其分布、随机变量的数字特征、大数定律与中心极限定理、样本及抽样分布、参数估计、假设检验等,注重概率模型构建与统计推断能力。 | 不考察 | 与数学一基本一致,但侧重点不同:如二维随机变量仅要求常见分布(二维正态分布不要求),假设检验仅要求单个正态总体的均值与方差检验,更注重统计方法在经济问题中的应用(如回归分析、参数估计)。 |
难度差异:综合能力与思维层次的要求不同
数学二、数学三的难度并非仅体现在“题量”或“计算量”上,更体现在对数学思维、知识综合应用能力的要求差异上,整体难度排序为:数学一 > 数学三 > 数学二。
数学一是三者中难度最高的,原因在于:
- 知识范围广:涉及高等数学的全部模块(含多元微积分、无穷级数、微分方程)、线性代数的全部核心考点及概率论与数理统计的完整体系;
- 理论要求深:如高等数学中要求掌握中值定理的多种证明方法、多元函数极值的充分必要条件;线性代数中要求理解向量空间、线性变换等抽象概念;概率论中要求掌握多维随机变量的分布函数、协方差矩阵等复杂内容;
- 综合应用强:题目常涉及多个知识点的交叉,如结合微积分与线性代数求解优化问题,或利用概率论知识解决实际模型问题,对考生的逻辑推理和灵活运用能力要求极高。
数学三的难度次之,虽然高等数学范围与数学一接近,但:
- 理论深度降低:如多元函数微积分不要求三重积分的物理应用,无穷级数不涉及傅里叶级数展开,概率论中不要求特殊分布(如伽马分布、贝塔分布)的细节;
- 侧重应用导向:题目更贴近经济管理实际,如利用导数求边际成本、弹性系数,利用概率知识计算风险收益,利用统计方法进行数据分析等,对抽象思维要求较低,但对“数学建模-求解-解释”的能力要求较高。
数学二难度相对最低,主要因:
- 知识范围窄:不考察概率论与数理统计,高等数学仅保留基础模块(一元微积分、多元微积分基础、常微分方程基础);
- 计算为主,理论为辅:题目以常规计算和简单应用为主,如一元函数的极值、最值,多元函数的偏导数计算,线性代数的矩阵运算、方程组求解等,较少涉及复杂的理论证明和综合应用题。
备考建议:针对性规划,高效复习
- 明确考纲,聚焦重点:根据报考专业确定考试类型后,需严格对照最新考研数学大纲梳理考点,避免“超纲复习”或“漏考点”,数学二考生需彻底放弃无穷级数和概率论,数学三考生需重点掌握经济应用类题型(如边际分析、统计检验)。
- 强化基础,注重方法:无论是数学一、二还是三,基础题占比均达60%以上,需优先吃透基本概念(如导数的定义、矩阵的秩)、基本公式(如泰勒展开式、线性方程组求解公式)和基本方法(如换元积分法、特征值求解法)。
- 综合训练,突破难点:数学一和数学三考生需加强知识点综合训练,如微积分与线性代数的结合(利用特征值求解微分方程)、概率论与统计的应用(利用中心极限定理进行近似计算);数学二考生需提升计算准确率,避免因粗心丢分。
- 真题导向,模拟实战:近10年真题是备考的核心资源,需通过真题分析命题趋势、高频考点及难度分布,同时定期进行模拟考试,适应考试节奏(如数学一考试时长3小时,题量较大,需合理分配时间)。
相关问答FAQs
Q1:数学一和数学三的高等数学部分内容几乎相同,如何区分复习重点?
A:虽然两者高等数学模块章节名称相似,但侧重点差异显著,数学一更注重理论深度和综合应用,如多元函数微积分中的三重积分计算、曲线曲面积分的物理应用(通量、环流),无穷级数中的傅里叶级数展开,常微分方程中的可降阶方程求解等;数学三则侧重经济应用,如利用定积分求平面图形面积(经济模型中的收益、成本曲线)、利用偏导数求多元函数的极值(利润最大化模型),且不要求三重积分、傅里叶级数等内容,复习时,数学一考生需强化复杂计算和理论证明,数学三考生需专注经济应用题型的建模与求解。
Q2:数学二不考概率论与数理统计,是否意味着复习时可以完全放弃?
A:数学二确实不考察概率论与数理统计,但需注意“不考”不等于“不学”,线性代数和高等数学中部分知识点与概率论存在交叉(如矩阵运算在随机变量协方差计算中的应用,微积分在概率密度函数积分中的应用),虽然数学二不直接考概率,但理解这些关联有助于加深对数学整体框架的认知,数学二的考试时长为3小时,题量相对较少(通常22题左右),若完全放弃概率论,可能导致复习时间分配失衡,建议将节省的时间用于强化高等数学和线性代数的薄弱环节,确保基础题和中档题的得分率。