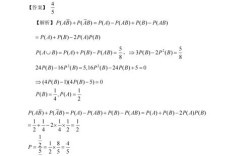2025年考研数学二真题作为当年研究生入学考试的重要参考,其命题特点、考点分布及难度水平对后续备考具有深远影响,该试卷整体难度适中,注重对基础知识、基本技能及综合应用能力的考查,尤其强调对数学核心概念的理解与灵活运用,以下从试卷结构、典型题型解析及备考启示三个方面展开分析。

试卷结构与考点分布
2025年考研数学二试卷满分为150分,包括高等数学(约78%)、线性代数(约22%)两大部分,题型涵盖选择题(8小题,每题4分)、填空题(6小题,每题4分)和解答题(9小题,共94分),具体考点分布如下:
| 学科 | 章节 | 考查重点 |
|---|---|---|
| 高等数学 | 极限与连续 | 洛必达法则、泰勒展开、数列极限与函数极限的关系 |
| 一元函数微分学 | 导数定义、隐函数求导、微分中值定理的应用 | |
| 一元函数积分学 | 定积分计算、反常积分收敛性、积分上限函数的性质 | |
| 多元函数微分学 | 偏导数计算、全微分形式不变性、方向导数与梯度 | |
| 常微分方程 | 一阶微分方程求解、二阶常系数线性微分方程解的结构 | |
| 线性代数 | 行列式与矩阵 | 矩阵运算、逆矩阵、矩阵的秩 |
| 线性方程组 | 克拉默法则、解的结构、基础解系 | |
| 特征值与特征向量 | 特征值计算、相似矩阵、二次型标准化 |
典型题型深度解析
选择题第8题(极限计算)求极限 (\lim_{x \to 0} \frac{\ln(\cos x)}{x^2})。
解析:本题考查泰勒展开与等价无穷小替换的结合使用,当 (x \to 0) 时,(\cos x \approx 1 - \frac{x^2}{2}),(\ln(\cos x) \approx \ln(1 - \frac{x^2}{2}) \approx -\frac{x^2}{2}),代入原式得极限为 (-\frac{1}{2}),考生若直接使用洛必达法则,需两次求导,计算量较大,易出错。
解答题第16题(积分与微分方程综合)设函数 (f(x)) 在 ([0,1]) 上连续,且满足 (\int_0^x f(t) \, dt = x \int_0^1 f(x) \, dx - \frac{x^3}{3}),求 (f(x))。
解析:本题通过积分方程构造微分方程求解,对等式两边关于 (x) 求导,得 (f(x) = \int_0^1 f(x) \, dx - x^2),令 (c = \int_0^1 f(x) \, dx),则 (f(x) = c - x^2),代入积分表达式得 (c = \int_0^1 (c - x^2) \, dx = c - \frac{1}{3}),解得 (c = \frac{1}{3}),(f(x) = \frac{1}{3} - x^2)。
线性代数解答题(特征值与二次型)已知二次型 (f(x_1, x_2, x_3) = x^T A x) 的秩为2,且 (A) 的各行元素之和为0,求该二次型的规范形。
解析:由“各行元素之和为0”可知 ((1,1,1)^T) 是 (A) 的特征向量,对应特征值为0,因秩为2,故0为二重特征值,另一特征值由迹确定,设非零特征值为 (\lambda),则 (\text{tr}(A) = \lambda),通过特征值符号判断规范形:若 (\lambda > 0),规范形为 (y_1^2 + y_2^2);若 (\lambda < 0),规范形为 (-y_1^2 - y_2^2),本题需进一步计算 (\lambda) 的符号,但核心在于理解特征值与二次型标准化的关系。
备考启示与策略
- 基础概念优先:真题中约60%的题目直接考查基本概念(如导数定义、矩阵秩、特征值等),需熟练掌握定义、定理及推导过程。
- 方法灵活应用:同一问题可能有多种解法(如极限计算中的泰勒展开与洛必达法则),需通过真题训练优化解题路径。
- 综合能力提升:解答题常涉及跨章节知识(如积分与微分方程结合、线性代数与高等数学交叉),需构建知识网络。
- 计算准确性:填空题和解答题对计算精度要求高,需加强代数运算与符号推导的练习。
相关问答FAQs
Q1:2025年数学二真题中,哪些章节是高频考点?
A1:高频章节包括高等数学的极限与连续、一元函数微分学、常微分方程,以及线性代数的行列式与矩阵、线性方程组、特征值与特征向量,微分中值定理、积分计算、二次型标准化几乎每年必考,需重点复习。
Q2:如何有效利用真题进行备考?
A2:建议分三阶段使用真题:① 按章节分类练习,针对性突破薄弱点;② 模拟考试环境限时训练,提升解题速度;③ 分析错题,归纳错误类型(如概念混淆、计算失误),并回归教材巩固基础,可对比近5年真题,总结命题趋势,如线性代数解答题对“秩与特征值”的考查频率逐年上升。