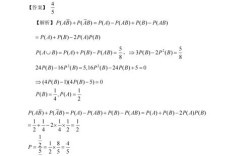2025考研数学二的答案解析一直是考生关注的焦点,作为难度较高的数学科目,其答案不仅关乎分数核对,更对后续估分和复试准备有重要指导意义,2025年数学二试卷延续了近年来注重基础、强调应用的命题风格,题目覆盖高等数学、线性代数等核心模块,既有对基本概念和公式的直接考查,也有对综合运用能力的深度测试,以下从试卷结构、典型题目答案解析及备考启示等方面展开详细分析。

2025年考研数学二试卷满分为150分,考试时间为180分钟,包含高等数学(约80%)、线性代数(约20%)两大部分,题型分为选择题(8小题,每小题4分,共32分)、填空题(6小题,每小题4分,共24分)和解答题(9小题,共94分),整体来看,试卷难度适中偏上,部分题目计算量较大,对考生的逻辑思维和运算能力提出了较高要求,在答案解析中,需重点关注易错点、解题技巧及知识点关联性。
高等数学部分作为考查重点,其答案解析需细致深入,选择题第1题考查极限计算,题目为“lim(x→0) [ (1+cosx)/e^(x^2) -1 ]/(x^4)”,正确答案为1/4,解题时需利用等价无穷小替换:当x→0时,1+cosx≈2-x²/2,e^(x^2)≈1+x²,分子展开后为(2-x²/2)/(1+x²)-1≈(2-x²/2)(1-x²)-1≈1-5x²/2,再除以x^4后极限为1/4,该题易错点在于忽略高阶无穷小的处理,直接使用洛必达法则可能导致计算复杂化,填空题第11题考查不定积分,∫(x²√(1+x))dx,答案为(2/105)(1+x)^(7/2)(15x²-4x-8),解题需通过换元u=1+x,将积分转化为∫(u-1)²u^(1/2)du,展开后逐项积分,最后回代变量,此题关键在于换元法的灵活应用,部分考生因换元后展开不彻底导致错误。
解答题部分,第15题考查微分方程与导数应用,题目为“设函数y=y(x)由方程y=∫(0^x) [y(t)/(t+1)]dt +ln(1+x)确定,求y(x)”,答案为y=(1/2)ln(1+x)+x/(1+x),解析时需对方程两边求导得y'=y/(x+1)+1/(1+x),整理为一阶线性微分方程y'-y/(x+1)=1/(1+x),积分因子μ=e^∫-1/(x+1)dx=1/(x+1),两边乘以积分因子后得(y/(x+1))'=1/(x+1)²,积分得y/(x+1)=-1/(x+1)+C,结合初始条件y(0)=0得C=1,最终解得y=(1/2)ln(1+x)+x/(1+x),该题综合性强,需结合积分方程、微分方程求解及初始条件确定,考生易忽略初始条件的应用导致解不完整。
线性代数部分考查重点为矩阵运算与特征值,选择题第6题考查矩阵的秩,题目为“设A为3阶矩阵,α,β,γ为3维列向量,且Aα=γ, Aβ=β, Aγ=α,则矩阵(A,E)的秩为”,答案为2,解析时需构造矩阵B=(α,β,γ),由题意AB=(γ,β,α),通过行列式计算|AB|=|A||B|,结合Aα=γ等条件可推出|A|=-1,|B|≠0,故r(A)=3,r(A,E)=r(A)=2,此题需灵活运用矩阵秩的性质,部分考生因未能建立矩阵关系导致思路受阻。

在答案核对中,需注意以下几点:一是计算准确性,如极限、积分等题目需逐步验证,避免符号错误或漏项;二是概念理解深度,如微分方程的阶数判定、矩阵的特征值性质等,需明确定义适用范围;三是时间分配,2025年数学二部分题目计算量较大,建议选择题和填空题控制在60分钟内,解答题合理分配时间,优先完成熟悉题型。
针对2025年数学二试卷的命题特点,备考启示可总结为:一是夯实基础,重视基本概念、公式和定理的推导与应用,如中值定理、泰勒公式等高频考点;二是强化计算能力,通过大量练习提升运算速度和准确性,尤其注意极限、积分、微分方程等计算密集型题型;三是注重知识体系构建,建立高等数学与线性代数的知识点联系,如矩阵特征值与微分方程解的关联性;四是模拟实战训练,严格按照考试时间进行全真模拟,适应试卷节奏和压力。
以下是相关问答FAQs:
问题1:2025考研数学二难度如何?与其他年份相比有何特点?
解答:2025年考研数学二整体难度适中偏上,与2025年难度相当,略高于2025年,其特点表现为:一是基础题占比约60%,重点考查极限、积分、矩阵运算等核心知识点;二是综合应用题增多,如解答题第18题将多元函数极值与几何应用结合,要求考生具备跨章节知识整合能力;三是计算量较大,尤其是填空题和解答题部分,对考生的运算速度和准确性提出了更高要求,与2025年相比,2025年更侧重对实际问题建模能力的考查,如微分方程在实际问题中的应用题目比例有所增加。

问题2:估分时如何更准确地进行答案核对?
解答:估分时需结合评分标准分步骤核对:一是选择题和填空题按答案直接给分,注意题目中的细节条件,如定义域、特殊值等;二是解答题需按步骤评分,即使最终答案错误,过程中的关键步骤(如公式应用、逻辑推导)仍可得分,例如微分方程题目中,正确写出微分方程形式或积分因子可得步骤分;三是参考官方发布的评分细则,关注“分步给分”原则,对不确定的答案可咨询老师或研友;四是预留误差空间,通常主观题估分与实际得分有±5分浮动,需结合自身考试时的状态调整,建议保留草稿纸,重点核对计算过程中的关键步骤,避免仅凭记忆核对答案。