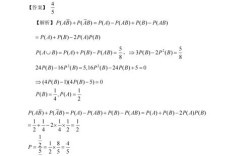2010年考研数学二真题作为当年研究生入学考试的重要参考,其命题特点、考点分布及难度水平对后续备考具有深远影响,该试卷整体结构严谨,涵盖高等数学、线性代数两大核心模块,注重对基础知识综合应用能力与计算能力的双重考查,以下从试卷结构、典型题型解析及备考启示三个方面展开详细分析。

试卷结构方面,2010年数学二真题共23道题,满分150分,考试时间180分钟,其中选择题8道(每题4分,共32分),填空题6道(每题4分,共24分),解答题9道(共94分),高等数学部分占比约78%,包括极限、导数与微分、中值定理、积分、微分方程等内容;线性代数部分占比约22%,主要涉及行列式、矩阵、向量、线性方程组及特征值与特征向量,这种分值分配延续了数学二“重高数、轻线代”的传统特点,但线性代数部分仍注重知识点的内在联系,如2010年真题中矩阵运算与线性方程组解的结构结合考查,体现了对综合能力的重视。
典型题型解析中,高等数学部分的第一题为极限计算题,考查了等价无穷小替换与洛必达法则的结合应用,属于基础但易失分的题型,题目为求(\lim{x \to \infty} \left( \frac{x^2}{(x-a)(x+b)} \right)^x),考生需通过变形后利用(\lim{x \to \infty} \left(1+\frac{1}{x}\right)^x=e)的结论求解,此题凸显了对基本极限公式灵活运用能力的考查,微分方程部分则出现了二阶常系数非齐次线性微分方程的求解,题目为(y''-3y'+2y=e^{x}\sin x),需先求齐次方程通解,再通过待定系数法确定特解,过程中涉及三角函数与指数函数乘积的特解设定,对计算准确性要求较高,线性代数部分的一道矩阵题通过已知矩阵方程(AB=A+2B)求解矩阵B,考查了矩阵的初等变换与逆矩阵运算,考生需先通过方程变形得到((A-2E)B=A),再验证(A-2E)的可逆性后求解,此类问题强调对矩阵运算性质的深刻理解。
难度分布上,2010年数学二真题呈现“梯度明显、重点突出”的特点,选择题与填空题以基础概念和简单计算为主,如导数定义、积分基本公式等,约占40%的分值;解答题前3题为常规题型,考查基本方法的应用;中间3题难度提升,如多元函数极值问题,需结合拉格朗日乘数法,计算量较大;最后3题为综合压轴题,涉及曲线积分与曲面积分的综合应用,要求考生具备较强的空间想象与逻辑推理能力,整体来看,试卷区分度较高,既保证了基础题的得分率,又为优秀考生提供了发挥空间。
备考启示方面,2010年真题反映出三个核心方向:一是夯实基础概念,如中值定理的五个条件、线性相关性的定义等,需做到精准记忆;二是强化计算能力,尤其是积分运算、矩阵变换等步骤,需通过大量练习减少失误;三是注重知识串联,如微分方程与级数的综合、线性方程组解与特征向量的关联等,建议考生在复习时建立“知识点-题型-方法”的思维导图,针对高频考点(如极限、积分、矩阵特征值)进行专项突破,同时通过限时训练提升应试速度与准确率。

相关问答FAQs:
Q1:2010年考研数学二真题中,线性代数部分占比约22%,是否意味着可以适当减少复习时间?
A1:不建议,虽然线性代数分值占比低于高等数学,但其知识点相对集中,且题型具有较强规律性,特征值与特征向量、线性方程组解的结构等内容常与高等数学综合考查(如微分方程组的求解),若基础薄弱,可能导致该部分失分过多,反而拉低总分,建议合理分配时间,确保线性代数核心知识点(行列式、矩阵、向量、方程组、特征值)的熟练掌握,注重题型归纳与解题模板的总结。
Q2:针对2010年真题中计算量较大的解答题(如多元函数极值、曲线积分),如何提升解题效率?
A2:提升效率需从“方法优化”与“步骤规范”两方面入手,掌握常用解题技巧,如多元函数极值问题中,优先简化目标函数(如取对数、变量替换)以减少计算量;曲线积分则需灵活选择格林公式或直接参数化,根据积分路径与被积函数特点判断最优方法,规范答题步骤,明确关键得分点(如拉格朗日乘数法的方程建立、曲线积分的方向判断),避免冗余计算,平时练习时建议限时训练,模拟考场压力,同时建立错题本,针对易错步骤(如符号错误、公式记错)进行针对性强化。