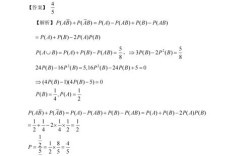2010年考研数学真题作为全国硕士研究生入学统一考试的重要组成部分,其命题特点、考查重点及对后续备考的指导意义值得深入分析,该年度数学试卷分为数学一、数学二、数学三三个类别,各自针对不同学科门类的考生需求,但整体均注重对基础知识、基本技能和综合应用能力的考查。

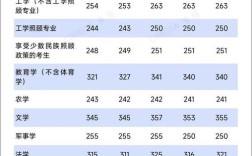
从试卷结构来看,2010年数学一包含高等数学(56%)、线性代数(22%)和概率论与数理统计(22%)三部分;数学二侧重高等数学(78%)和线性代数(22%);数学三则涵盖微积分(56%)、线性代数(22%)和概率论与数理统计(22%),各题型分布为选择题(8小题,每题4分)、填空题(6小题,每题4分)和解答题(9小题,共94分),总分150分,考试时长180分钟,这种结构延续了历年考研数学的经典模式,强调知识点的全面覆盖与重点突出。
在高等数学(或微积分)部分,2010年真题注重对核心概念和定理的深入理解,数学一中极限的计算题涉及等价无穷小替换、洛必达法则及泰勒展开的综合应用,要求考生不仅掌握方法,更要灵活选择最优路径,微分方程的考查则结合了物理背景,如利用牛顿第二定律建立微分方程并求解,体现了数学建模能力的重要性,多元函数积分学中的曲线积分与曲面积分计算,对考生空间想象力和运算技巧提出了较高要求,如高斯公式、斯托克斯公式的灵活运用是得分关键。
线性代数部分,2010年各卷种均突出了对知识体系综合性的考查,行列式、矩阵、向量、线性方程组及特征值等章节内容交叉融合,例如通过矩阵的秩判断线性方程组解的情况,或利用特征值、特征向量反推矩阵参数,数学三中还出现了二次型标准化与合同变换的结合题,要求考生熟练掌握正交变换法配方法,并理解其几何意义,此类题目往往需要多步推理,对逻辑严谨性要求较高。
概率论与数理统计部分,2010年真题延续了理论与实际应用结合的特点,随机变量及其分布的考查涉及离散型与连续型变量的联合分布、边缘分布及相关性判断,如二维均匀分布的概率计算,数理统计部分则重点围绕参数估计(矩估计、最大似然估计)和假设检验(t检验、χ²检验)展开,数学三中还增加了区间估计的题目,要求考生掌握统计量的构造及分布性质,整体来看,概率部分公式繁多,但考查核心仍在于概念辨析与公式适用场景的判断。

针对备考策略,2010年真题反映出以下启示:一是基础知识的扎实掌握至关重要,如极限、导数、积分的基本计算必须做到快速准确;二是知识点的串联能力,例如微分方程与物理应用、线性代数与空间解析几何的结合;三是计算能力的提升,尤其是复杂运算的耐心与细心,避免因粗心丢分,建议考生在复习时以教材为核心,构建知识网络,并通过真题训练把握命题规律,总结解题方法。
以下是相关问答FAQs:
Q1:2010年考研数学真题中,哪些题目属于高频考点?
A1:2010年真题的高频考点包括:极限计算(等价无穷小、洛必达法则)、微分方程求解(可分离变量、二阶常系数线性微分方程)、多元函数积分学(曲线积分、曲面积分)、线性代数中的特征值与特征向量、线性方程组解的结构,以及概率论中的随机变量分布函数、参数估计(矩估计与最大似然估计),这些知识点在近十年考研数学中反复出现,是复习的重点。
Q2:如何有效利用2010年考研数学真题进行备考?
A2:利用2010年真题备考可分三步:一是模拟实战,严格按照考试时间和流程完成试卷,检验时间分配与应试状态;二是深度分析,对错题归类,查找知识漏洞(如概念混淆、计算失误),并归纳同类题型的通用解法;三是拓展延伸,以真题为线索,回归教材巩固相关知识点,通过变式训练强化薄弱环节,同时关注命题趋势(如应用题、综合题的比重变化)。