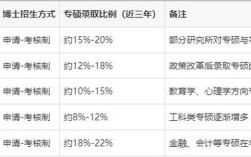
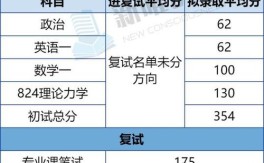
浙江大学物理系作为国内物理学研究的重镇,其博士研究生入学考试（简称“考博”）真题不仅是考生备考的核心资料，也折射出学科的前沿方向与学术要求，以下从真题特点、核心考点、备考策略及典型题型解析等方面展开详细分析，帮助考生系统把握备考方向。

浙江大学物理系考博真题的核心特点

浙江大学物理系考博真题注重对考生基础理论深度、科研思维及综合应用能力的考察，具体表现为以下三点：

1. 基础性与前沿性结合
   真题既涵盖经典物理的核心理论（如电动力学、量子力学、热力学与统计物理的基础概念与推导），也融入当前研究热点（如量子计算、凝聚态物理中的拓扑物态、光学中的超快激光等），量子力学部分常涉及角动量耦合、微扰理论的高级应用，同时结合量子信息中的量子态调控问题；凝聚态物理可能要求结合能带理论分析拓扑绝缘体的表面态。

2. 数学工具与物理模型的综合运用
   物理学研究高度依赖数学工具，真题中常出现需通过微分方程、特殊函数、群论等解决问题的场景，电动力学中要求用格林函数求解边值问题，统计物理中需运用系综理论推导相变临界指数，这对考生的数学应用能力提出较高要求。

3. 科研导向与开放性思维 以当前研究课题为背景，要求考生设计实验方案或解释物理现象的机制。“如何利用扫描隧道显微镜（STM）研究单分子磁性的磁矩翻转行为？”这类问题没有标准答案，考察考生对实验原理的理解、逻辑推理及创新思维。

   
   （图片来源网络，侵删）

核心考点及典型题型解析

浙江大学物理系考博一般分为专业基础课（如量子力学、电动力学、热力学与统计物理）和专业课（按研究方向分为凝聚态物理、光学、粒子物理等），以下分模块梳理核心考点及题型。

（一）量子力学

量子力学是物理系考博的绝对核心,占比通常达30%-40%，考点集中在以下方面：

• 基本原理与形式体系：态矢量、算符对易关系、不确定性原理的深入理解，题目可能要求证明“坐标算符与动量算符的对易关系”，并推导其在球坐标下的表达式。
• 近似方法：定态微扰理论（如简并微扰的应用）、变分法（用于求解复杂体系的基态能量）、非微扰方法（如WKB近似），典型题型如“用变分法估算氦原子基态能量，尝试试探波函数的形式”。
• 对称性与角动量：旋转对称性、空间反演对称性对能级的影响，角动量耦合（LS耦合与jj耦合），题目可能给出某体系的哈密顿量，要求分析其对称性导致的能级简并。
• 前沿专题：量子纠缠（如Bell不等式的实验验证）、量子计算（量子门操作、量子纠错）、开放量子系统（主方程方法）。

典型例题：
“设一维谐振子受到微扰Hamiltonian ( H' = \lambda x^4 )（(\lambda)为小量），用微扰理论计算基态能量的一级修正。”
解析：需先写出无微扰时的基态波函数 (\psi_0(x) = \left(\frac{m\omega}{\pi\hbar}\right)^{1/4} e^{-m\omega x^2/2\hbar})，然后计算一级修正 ( E_0^{(1)} = \langle \psi_0 | H' | \psi_0 \rangle )，通过积分利用 Hermite 多项式的性质求解。

（二）电动力学

电动力学考察电磁场理论的核心框架及与近代物理的结合,重点包括：

• Maxwell 方程组的积分与微分形式：边界条件（如导体表面、介质界面的电磁场关系）、电磁势规范（库仑规范与洛伦兹规范的选择）。
• 电磁波传播：平面电磁波在介质中的传播（色散与吸收）、波导中的模式分析、辐射场（电偶极辐射的辐射功率与角分布）。
• 相对论电动力学：四维协变量（四维动量、电磁场张量）、相对论性多普勒效应。
• 专题应用：超材料中的负折射、等离子体中的电磁波传播。

典型例题：
“半径为 ( a ) 的导体球置于均匀静电场 ( \mathbf{E}_0 = E_0 \hat{z} ) 中，求球外的电势分布及球面上的电荷面密度。”
解析：采用分离变量法求解 Laplace 方程，结合边界条件（球面电势为常数、无穷远处电势为 (-E_0 r \cos\theta)），得到电势解后，通过 ( \sigma = -\epsilon0 \frac{\partial \phi}{\partial r} \big|{r=a} ) 计算电荷面密度。

（三）热力学与统计物理

该模块注重热力学定律的宏观表述与统计物理的微观诠释,核心考点为：

• 热力学基本定律：热力学第一定律的应用（如循环效率计算）、Maxwell 关系及其应用（如推导绝热压缩系数与等温压缩系数的关系）。
• 统计物理方法：系综理论（微正则系综、正则系综、巨正则系综的配分函数计算）、玻色-爱因斯坦与费米-狄拉克统计（如 Bose-Einstein 凝聚的条件）。
• 相变与临界现象：Ising 模型、平均场理论、临界指数与标度律。

典型例题：
“由 ( N ) 个单原子分子组成的理想气体，满足经典统计，求其在正则系综下的配分函数 ( Z )，并推导内能 ( U ) 和压强 ( P )。”
解析：单原子分子配分函数 ( Z = Z{\text{平动}} \cdot Z{\text{内}} )，其中平动配分函数 ( Z{\text{平动}} = \left(\frac{2\pi mkT}{h^2}\right)^{3/2} V )，内配分函数 ( Z{\text{内}} = 1 )（忽略电子激发），再通过 ( U = -\frac{\partial \ln Z}{\partial \beta} )、( P = kT \frac{\partial \ln Z}{\partial V} ) 推导结果。

（四）专业课（以凝聚态物理为例）

凝聚态物理是浙大物理系的强势方向,考博真题常涉及：

• 晶体结构与能带理论：倒格子、Bragg 反射、紧束缚模型与近自由电子模型。
• 磁性理论：Heisenberg 模型、铁磁体的自发磁化、量子相变。
• 低维物理：量子霍尔效应、石墨烯的 Dirac 点能带、拓扑绝缘体。

典型例题：
“用紧束缚模型描述石墨烯中碳原子的 ( p_z ) 轨道，推导其能带结构，并说明 Dirac 锥的成因。”
解析：需建立石墨烯的 honeycomb 晶格模型，写出 hopping Hamiltonian，通过 Fourier 变换得到动量空间的哈密顿量，对角化后得到 ( E(\mathbf{k}) = \pm t \sqrt{3 + 2\cos(\sqrt{3} k_y a) + 4\cos(\frac{3}{2} k_x a)\cos(\frac{\sqrt{3}}{2} k_y a)} )，在 ( K ) 点附近线性化即得 Dirac 锥。

备考策略与资源推荐

1. 夯实基础，吃透教材
   核心教材包括：量子力学（曾谨言《量子力学教程》）、电动力学（郭硕鸿《电动力学》）、统计物理（汪志诚《热力学·统计物理》），需精读教材并完成所有习题，重点掌握公式推导的物理意义而非死记硬背。

2. 真题演练与专题突破
   收集近5-10年浙大物理系考博真题，按模块分类整理，针对高频考点（如量子力学微扰理论、电动力学边值问题）进行专项训练，对于开放性题目，多参考《Physical Review》《Nature Physics》等期刊的前沿综述，培养科研思维。

3. 关注学科前沿，联系导师方向
   浙大物理系各研究组（如量子信息、凝聚态理论、光学）的近期论文可能成为考题来源，建议提前阅读目标导师的代表性论文，理解其研究方法与核心结论，面试时更容易展现匹配度。

4. 数学工具强化
   重点复习《数学物理方法》（梁昆淼），掌握特殊函数（Legendre、Hermite、Laguerre 多项式）、积分变换、偏微分方程求解等，避免因数学能力不足影响物理问题的解答。

相关问答FAQs

Q1：浙江大学物理系考博是否需要提前联系导师？联系导师时应该注意什么？
A1：建议提前联系导师，联系时需注意：① 邮件主题明确（如“考博咨询-姓名-研究方向”），内容包括个人教育背景、科研经历（如参与的项目、发表的论文）、对导师研究方向的兴趣及理解；② 态度诚恳，避免空泛吹嘘，可附上本科/硕士成绩单、简历等材料；③ 若导师回复积极，可进一步询问是否推荐阅读其论文或组会文献，体现主动性。

Q2：考博面试中，如果遇到不会的专业问题，应该如何应对？
A2：面试遇到不会的问题时，切忌沉默或胡乱回答，建议采取以下策略：① 诚实表示对该问题的理解有限，但尝试从相关基础理论出发进行分析，这个问题我目前了解不深，但根据XX理论，我推测可能涉及XX机制，是否可以这样理解……”；② 若问题涉及某个具体公式或模型，可请求提示，如“能否提示一下该问题的关键步骤？”；③ 展现学习能力，可补充“这个问题我会后续查阅文献深入学习，感谢老师的指导”，诚实且积极的态度往往比正确答案更重要。